Bộ lọc Kalman

[falleaf]

Ai có nhu cầu Kalman thì bay vô đây chơi... Mở ra nhưng lười viết bài quá, ai quan tâm thì F sẽ post một số tài liệu lên cho mọi người xem chơi..

F rất khôn, điều khiển thì chỉ học PID, mạch lọc thì chỉ học Kalman ...

Tài liệu tham khảo:
[1] Introduction to Random Signals and Applied Kalman Filtering của Brown và Hwang: http://www.tailieuvietnam.net/download/Kalman/Brown.pdf
[2] http://www.cs.unc.edu/~welch/kalman/index.html

[falleaf]

Đọc một bài báo đơn giản sử dụng Indirect Kalman Filter

www.picvietnam.com/download/Kalman/PRE01.pdf

Đây là một báo cáo nói trong 5 phút về một bài báo liên quan đến Kalman. Đơn giản thôi, nhưng bài báo này tổng hợp cả phương pháp UMBmark, vì vậy, phải nắm bắt thật kỹ phương pháp UMBmark thì mới hiểu được bài báo này.

Điều quan trong nhất trong việc thực hiện một bộ lọc Kalman, đó là mô hình hóa được hệ thống. Vì vậy, trong bài báo cáo này, F chỉ dừng lại ở việc chỉ ra mô hình hóa của hệ thống.

Từng bước, F sẽ viết nhiều hơn về cái này, từ cơ bản. Nhưng trước tiên, các bạn chỉ cần nắm, làm việc với mạch lọc Kalman, tức là tìm ra mô hình của hệ thống.

Chúc vui.

[falleaf]

Bộ lọc Kalman

1. Bộ lọc Kalman là gì?

Đầu tiên, bộ lọc Kalman là bộ lọc do một cái ông nào đó có tên Kalman nghĩ ra, ỗng sống chết thế nào không cần biết, mặt mũi ỗng thế nào không cần hay. Chỉ cần biết ỗng chế ra một bộ lọc dùng được, nên lấy tên mình đặt cho bộ lọc. Nhưng nói vậy chứ, ai tò mò muốn biết thì vào đây coi. Cực kỳ đẹp trai.

http://www.ieee.org/organizations/hi...es/kalman.html

1.1. Bộ lọc là gì?

Bộ lọc là cái đồ để lọc, có nghĩa là có một thứ dơ bẩn nào đó, bỏ vào thì nó giữ lại những cái dơ và cho ra những cái sạch ở đầu bên kia.

Thiệt ra thì F về nhà hỏi bà nội F làm sữa đậu nành thế nào mới biết cái bộ lọc chỉ là cái miếng vải may lại rồi cứ thế đổ nước đậu và bã đậu vào.. cuối cùng bã đậu còn lại trong cái bị còn nước đậu chảy ra ngoài, hứng, nấu, khuấy đường... rồi uống.

1.2. Bộ lọc Kalman là gì?

Bộ lọc Kalman cũng là cái bịch vải của bà nội F thôi, nhưng mà ỗng không đổ bã đậu vào, mà ỗng đổ nhiễu tín hiệu vào đó, rồi có cả tín hiệu sạch, rồi đủ thứ hầm bà lằng trong đó, tóm lại là ỗng sẽ lấy ra được là tín hiệu sạch.

Tuy nhiên, cũng cần phải phân biệt rằng, cái vải lọc của bà nội F thì có lọc kiểu gì thì cũng là nước đậu, đâu có lọc ra nước tinh khiết được. Thế nên, tóm lại là cái bộ lọc Kalman cũng không hơn gì cái miếng vải của bà F, nó cũng chỉ lọc ra được tín hiệu sạch, theo nghĩa không còn nhiều nhiễu, nhưng cũng chỉ là ước lượng của tín hiệu thực, chứ không phải chính xác là tín hiệu thực.

Như vậy, người ta còn gọi bộ lọc Kalman là bộ lọc ước lượng, cũng vì lẽ đó.

Hôm nào rảnh lại viết tiếp, làm gì chứ nấu đậu nành chán lắm, tốt hơn là đi mua một ly đậu nành đá uống vẫn tốt hơn.

[falleaf]

Để tiện theo dõi, các bạn download tài liệu này về để tham khảo:

www.picvietnam.com/download/Kalman/Course1.pdf

Phần 2, F sẽ nói lại vấn đề học bộ lọc Kalman như thế nào? Ông thầy F giảng rất hay về bộ lọc Kalman, chính vì thế, F không muốn thay đổi nhiều trong bài giảng của ông ấy, nhưng về phần tự đọc, F sẽ cung cấp thêm cho các bạn một số tài liệu cần thiết, ngoài ra, F cũng sẽ cung cấp một số bài tập và bài giải liên quan đến mạch lọc Kalman. Mục tiêu để các bạn hiểu và nắm được mạch lọc này, đến mức có thể tự đọc tiếp về nó.

Những ai đã nghiên cứu và có kinh nghiệm sử dụng mạch lọc Kalman, xin giúp F một tay để bổ sung những thiếu sót trong quá trình biên soạn tài liệu này.

Cách học ở đây sẽ như thế nào? Mỗi tuần, F sẽ chỉ đưa lên một vấn đề nhỏ, và đưa tài liệu kèm theo, chỉ viết lại những ý chính cần thiết.

Vì các công thức toán đưa lên rất mất công, mà F lại toàn viết bằng Latex, cũng không chép lại lý thuyết khi làm nhiều, cho nên rất khó copy cho các bạn xem. Tuy nhiên, F sẽ cố gắng trình bày một cách cô đọng, nhưng đầy đủ nhất. Trong các tài liệu, cần xem chương nào, F cũng sẽ nói thật rõ chương nào cần xem.

Chúc vui.

[falleaf]

2. Học bộ lọc Kalman như thế nào?

2.1. Sơ kết

Chúng ta đã biết, bộ lọc chỉ đơn giản như trên, nhưng chúng ta chưa biết bộ lọc Kalman như thế nào?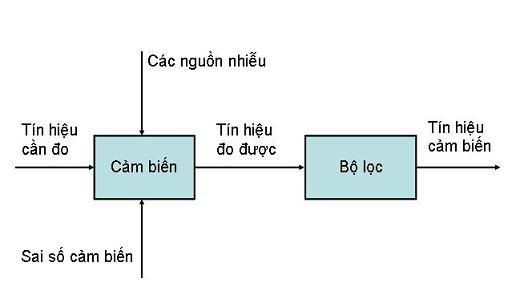

Thực ra nó cũng chỉ đơn giản là từ một tín hiệu cần đo, khi chúng ta đo, sẽ có những sai số từ cảm biến, ảnh hưởng đến tín hiệu cần đo, môi trường đo có nhiễu... Tất cả những thứ này, tổng hợp lại, sẽ cho ta một kết quả đo.

Nó cũng giống như chúng ta bỏ cả nước đậu, bã đậu, và tất tần tật mọi thứ vào trong một cái túi vải để lọc. Hình ảnh sau có vẻ sẽ thân thiện với các bạn hơn?

Chính vì vậy, học mạch lọc Kalman như thế nào?

Đây là một câu hỏi lớn không lớn, nhỏ không nhỏ, nhưng tính quan trọng của nó dành cho những người mới học là không thể chối cãi.

Chính vì vậy, F cũng đã được dạy phải học như thế nào, và ít ra thì F cũng đã học được một phần nào đó. Tuy chưa thể gọi là thấu đáo, tường tận, nhưng việc giúp các bạn có những ý tưởng cơ bản về mạch lọc Kalman, và bắt đầu nghiên cứu nó một cách phổ biến ở VN là điều F muốn làm.

Một hình ảnh đơn giản được đưa ra dưới đây để trả lời cho câu hỏi trên:

Ở đây F có mấy ý thay đổi theo cách giới thiệu, đó là F cho rằng các bạn chỉ cần ghi nhận, việc học xác suất, hiểu rõ nó, sẽ quyết định tất cả khi tìm hiểu về mạch lọc Kalman. Sau đó, F mới đi giải thích vì sao xác suất lại quyết định tất cả. Nhưng các bạn hãy tạo cho mình một niềm tin trước rằng, học bộ lọc Kalman hoàn toàn không khó. Thực tế F cũng học và hiểu được nó, chưa được hoàn chỉnh lắm, nhưng nó không quá khó và quá ghê gớm.

F cho rằng việc triển khai và ứng dụng mạch lọc Kalman ở VN là một việc làm đơn giản và dễ dàng. Chính vì vậy, F cung cấp thêm một cuốn sách nữa, để các bạn đọc sơ qua về xác suất.

F sẽ viết rất chậm, để các bạn có thời gian đọc về xác suất.

2.2. Một thí dụ nhỏ

Bây giờ F đưa ra một thí dụ sau, chúng ta lấy thước để đo chiều dài của một cây bút. Lần thứ nhất, chúng ta đo được là 10cm, lần thứ hai chúng ta đo được là 10.05cm chẳng hạn. Vậy thì nếu hỏi chiều dài cây bút là bao nhiêu?

Có phải trong đầu các bạn luôn cho một giá trị ước lượng tốt nhất là 10.025cm, có phải vậy không? Điều đó đúng, nhưng căn cứ vào đâu để các bạn ước lượng như vậy?

Rồi, nếu bây giờ, F lấy cây thước đo chiều dài, và được kết quả là 10.02 cm, và một bạn khác cũng lấy cây thước đo, và được chiều dài 10.07 cm. Nếu chỉ có hai kết quả này thôi, chúng ta sẽ lại ước lượng rằng chiều dài của cây thước là 10.045 cm. Đúng không nào?

Nhưng thực ra, nếu F cầm cây thước đo, cứ cho rằng, bạn kia là sinh viên đi, nếu thế thì rõ ràng kết quả đo của F sẽ đáng tin cậy hơn của một bạn sinh viên??? Còn nếu người kia là ông thầy F, thì các bạn sẽ tin ông thầy F hơn, đúng không???

Vậy thì, thực chất là không thể đánh đồng được chuyện đo đạc này, mà cần có một hệ số đánh giá.

Chiều dài cây thước là

chiều dài = alpha * 10.02 (của F đo) + (1-alpha)*10.07 (của người kia đo)

Vậy alpha sẽ là bao nhiêu? Căn cứ vào đâu để lựa chọn alpha?

F đã đưa ra một số ý tưởng phác thảo, để các bạn thấy được khái niệm về ước lượng. Phần sau, chúng ta sẽ nói rõ hơn và đưa ra một ví dụ rõ hơn, và lần sau chúng ta sẽ lấy ví dụ của thầy F để hiểu rõ vấn đề hơn.



Chúc các bạn ăn tết vui vẻ

[falleaf]

Vì diễn đàn còn một số trục trặc về trình bày, cho nên F tạm thời viết không có các chức năng display tốt, các bạn thông cảm.

2.3. Một thí dụ về ước lượng

Chúng ta giả sử, có một chiếc xe di chuyển với vận tốc 20m/s theo một phương x. Vị trí ban đầu của xe là 0.

Khi đó, vận tốc của xe sẽ là:

v_xe(t) = 20m/s + v_s(t)

Trong đó, v_s(t) là nhiễu vận tốc đo.

Kết quả, nếu bây giờ chúng ta cần xác định vị trí của xe sau 2 phút. Và nếu, chúng ta giải sử chúng ta chỉ quan tâm đến cảm biến đo vị trí hoặc cảm biến đo vận tốc của xe. Chúng ta sẽ chỉ ra được 2 phương pháp ước lượng như sau:

a) Phương pháp 1:

^x1(0) = z1 = 0
^x1(1) = z2 (thời điểm tiếp theo)
^x1(2) = z3 (thời điểm tiếp theo nữa)
....

Đây là ước lượng vị trí của xe, chỉ nhờ vào cảm biến vị trí của xe, trong đó, zi là các giá trị vị trí xe đo được.

b) Phương pháp 2:

^x2(0) = x(0) = 0 (vị trí ban đầu của xe)
^x2(1) = 0 + 20 (vị trí tiếp theo nếu giả sử xe di chuyển với vận tốc 20m/s)
^x2(2) = ^x(1) + 20 = 0 + 20 + 20 (tiếp theo nữa)
...

Như vậy, cả hai phương pháp trên, cũng đều là một cách để chúng ta ước lượng vị trí của xe.

Vậy áp dụng lại 2.2, chúng ta sẽ thấy rằng, nếu dùng hai phương pháp ước lượng khác nhau, chúng ta cũng sẽ có các giá trị ước lượng khác nhau. Chúng ta sẽ tin cách ước lượng nào hơn?...

c) Phương pháp 3:

Vậy thì, chúng ta thử xem phương pháp ước lượng thứ ba như sau:

^x3(i) = alpha*^x1(i) + (1-alpha)*^x2(i)

Vậy các bạn có nhận xét gì về cách ước lượng này?

Một cách chung chung (không phải là tổng quát, chỉ là khái niệm sơ khởi), nhiệm vụ của bộ lọc Kalman, chính là tìm ra hệ số alpha tối ưu để tìm ^x(t) gần đúng với x(t) nhất.

Vậy nhiệm vụ của mạch lọc Kalman được phát biểu rõ hơn một chút, đó là tìm ước lượng ^x(t) gần đúng với x(t) nhất (giá trị ước lượng gần đúng với giá trị thực tế nhất) thông qua hiểu biết của chúng ta về mô hình của hệ thống.

Chúc vui.

[vutiendungbkhn]

Nguyên văn bởi falleaf

Bộ lọc Kalman

1. Bộ lọc Kalman là gì?

Đầu tiên, bộ lọc Kalman là bộ lọc do một cái ông nào đó có tên Kalman nghĩ ra, ỗng sống chết thế nào không cần biết, mặt mũi ỗng thế nào không cần hay. Chỉ cần biết ỗng chế ra một bộ lọc dùng được, nên lấy tên mình đặt cho bộ lọc. Nhưng nói vậy chứ, ai tò mò muốn biết thì vào đây coi. Cực kỳ đẹp trai.

http://www.ieee.org/organizations/hi...es/kalman.html

1.1. Bộ lọc là gì?

Bộ lọc là cái đồ để lọc, có nghĩa là có một thứ dơ bẩn nào đó, bỏ vào thì nó giữ lại những cái dơ và cho ra những cái sạch ở đầu bên kia.

Thiệt ra thì F về nhà hỏi bà nội F làm sữa đậu nành thế nào mới biết cái bộ lọc chỉ là cái miếng vải may lại rồi cứ thế đổ nước đậu và bã đậu vào.. cuối cùng bã đậu còn lại trong cái bị còn nước đậu chảy ra ngoài, hứng, nấu, khuấy đường... rồi uống.

1.2. Bộ lọc Kalman là gì?

Bộ lọc Kalman cũng là cái bịch vải của bà nội F thôi, nhưng mà ỗng không đổ bã đậu vào, mà ỗng đổ nhiễu tín hiệu vào đó, rồi có cả tín hiệu sạch, rồi đủ thứ hầm bà lằng trong đó, tóm lại là ỗng sẽ lấy ra được là tín hiệu sạch.

Tuy nhiên, cũng cần phải phân biệt rằng, cái vải lọc của bà nội F thì có lọc kiểu gì thì cũng là nước đậu, đâu có lọc ra nước tinh khiết được. Thế nên, tóm lại là cái bộ lọc Kalman cũng không hơn gì cái miếng vải của bà F, nó cũng chỉ lọc ra được tín hiệu sạch, theo nghĩa không còn nhiều nhiễu, nhưng cũng chỉ là ước lượng của tín hiệu thực, chứ không phải chính xác là tín hiệu thực.

Như vậy, người ta còn gọi bộ lọc Kalman là bộ lọc ước lượng, cũng vì lẽ đó.

Hôm nào rảnh lại viết tiếp, làm gì chứ nấu đậu nành chán lắm, tốt hơn là đi mua một ly đậu nành đá uống vẫn tốt hơn.

Bang chủ nói hay ghê, tuyet voi do,rat don gian va di vao cuoc song,de hieu, pro

[benq]

Nguyên văn bởi falleaf

...
làm việc với mạch lọc Kalman, tức là tìm ra mô hình của hệ thống.
...
Chúc vui.

Falleaf đã lạc đề sang xác suất. Tôi xin trở lại vấn đề Falleaf nêu ra.

Falleaf "nói oan" cho bộ lọc Kalman rồi; lọc Kalman chỉ tìm ra trạng thái ước lượng của hệ thôi. Nói như bạn, hóa ra dùng bộ lọc Kalman, ta có thể tìm được mô hình của đối tượng à??? Nếu (A, B, C, D) là biểu diễn trạng thái của hệ, thì ta cần phải biết ma trận A, C mới thiết kế bộ lọc Kalman được chứ.

Trong điều khiển tối ưu, bộ lọc Kalman chính là bộ ước lượng trạng thái tối ưu (hay bộ quan sát trạng thái tối ưu). Mục tiêu của bộ quan sát là tìm vectơ trạng thái ước lượng sao x^ sao cho x^ bám theo x (x là vector trạng thái "thật").

Tại sao phải dùng bộ quan sát trạng thái?
Trong thiết kế bộ điều khiển phản hồi trạng thái u = -Kx, ban đầu người ta có giả thiết là tất cả các trạng thái đều đo được; sau đó dùng các phương pháp thiết kế (pole placement, LQR,...) để tìm ra K. Nhưng thực tế thường không dễ dàng đo được tất cả các trạng thái vì ko có đủ cảm biến, hơn nữa có thể có những trạng thái ko có ý nghĩa vật lý. Vì thế, người ta dùng bộ quan sát trạng thái, để từ đầu vào (u) đầu ra (y) của đối tượng, ta có thể ước lượng được những trạng thái không đo được. Tóm lại, đầu vào của bộ quan sát là u, y; đầu ra là x^ (ước lượng của x).

Ta thấy bài toán thiết kế bộ quan sát tương tự như bài toán thiết kế bộ điều khiển hồi tiếp trạng thái.
- Thiết kế bộ điều khiển: tìm ma trận K sao cho y bám theo y_đặt.
- Thiết kế bộ quan sát: tìm ma trận L sao cho x^ bám theo x.
Đây là 2 bài toán có tính đối ngẫu (duality).

Trong MATLAB nếu dùng 'place' để thiết kế bộ điều khiển thì ta cũng có thể dùng 'place' để thiết kế bộ quan sát bằng cách thay đổi tham số vào: A thay bằng A' (A chuyển vị), B thay bằng C'.Bằng cách chỉ định cực của bộ quan sát, ta có thể thay đổi cách x^ bám theo x như ý muốn. Trong trường hợp này ta có bộ quan sát Luenberger.

Trong trường hợp thiết kế bộ điều khiển tối ưu LQR, ta tìm K tối ưu cực tiểu hóa phiếm hàm J bằng cách giải 1 phương trình Riccati. Thông số thiết kế trong bài toán LQR là ma trận trọng số Q, R (xem tài liệu về LQR để biết cụ thể). Tương tự như vậy, nếu ta tìm được L tối ưu bằng cách giải 1 phương trình Riccati tương tự phương trình Riccati trên, thì ta sẽ được bộ quan sát trạng thái tối ưu. Đây chính là bộ lọc Kalman . "Thông số thiết kế" (tạm gọi như vậy) trong trường hợp này là W, V (covariance của nhiễu ngẫu nhiên).

Trong MATLAB, nếu dùng hàm 'lqr' để thiết kế bộ điều khiển tối ưu LQR, thì ta cũng có thể dùng 'lqr' để thiết kế bộ lọc Kalman bằng cách thay A bằng A', B bằng C', Q bằng W, R bằng V.

Nói thêm, LQR + bộ lọc Kalman = LQG (Linear Quadratic Gaussian).

Cụ thể thế nào thì các bạn tìm tài liệu đọc thêm.

Ghi chú: bộ quan sát trạng thái = bộ ước lượng trạng thái = bộ quan sát (nói tắt) = bộ ước lượng (nói tắt).

Keywords: Optimal control, LQR (Linear Quadratic Regulator), LQG (Linear Quadratic Gaussian), state feedback control, state observer, state estimator, Kalman filter, Luenberger filter.

[falleaf]

Xin giải thích rõ ý câu nói trên, bởi vì nguyên tắc thiết kế bộ lọc Kalman đã có sẵn và không phải là vấn đề khó. Cho nên, mấu chốt của bài toán bộ lọc Kalman, đó là phải có được mô hình của hệ thống.

Thành ra F mới nói, làm việc với bộ lọc Kalman, tức là tìm ra mô hình của hệ thống, bởi vì toàn bộ các vấn đề của bộ lọc Kalman đã được thực hiện khá đầy đủ. Bất kể khi nào người ta chỉ cần đưa ra A, B, C, D ở trạng thái rời rạc hoặc liên tục, đều có thể thiết kế được bộ lọc Kalman cho nó.

Có lẽ bạn hiểu nhầm ý của F ở trên thì phải.

Phần tiếp theo, có lẽ F sẽ đi thẳng vào vấn đề bộ lọc Kalman để tránh mất thời gian của các bạn, bởi vì phần đầu về xác suất là rất khó, khó cả cho người viết và khó cả cho người đọc, nhưng một nghịch lý là để hiểu nó thì lại không quá khó.

Chúc vui

[benq]

Nguyên văn bởi falleaf

...
Thành ra F mới nói, làm việc với bộ lọc Kalman, tức là tìm ra mô hình của hệ thống, bởi vì toàn bộ các vấn đề của bộ lọc Kalman đã được thực hiện khá đầy đủ. Bất kể khi nào người ta chỉ cần đưa ra A, B, C, D ở trạng thái rời rạc hoặc liên tục, đều có thể thiết kế được bộ lọc Kalman cho nó.
...
Chúc vui

Tôi đưa ra (A, B, C, D) nhưng hệ thống undetectable, bạn có thể thiết kế được bộ lọc Kalman không?

[falleaf]

Lúc nãy F có viết một bài trả lời chung chung, nhưng sau đó xoá đi. Thực sự, F rất muốn trả lời một cách hình thức, để không làm các bạn mới học phải cảm thấy khó khăn, nhưng sau đó lại nghĩ lại rằng, nếu như trả lời không thoả đáng cho bạn, thì chúng ta sẽ phải mất thời gian đi sâu vào đó quá. Mà hiện này, F không thể có đủ thời gian tập trung cho cả hai đề tài (vì đang làm bộ PID).

Do vậy, F trả lời luôn, mong rằng các bạn mới học, nếu tham khảo luồng này, có thể tạm bỏ qua các bài thảo luận này.

Trước tiên, xin nói về vấn đề viết tài liệu hướng dẫn. Bạn beng, nếu bạn đã hiểu biết về Kalman, rất mong bạn viết những bài viết chi tiết, và cụ thể, giúp đỡ các thành viên diễn đàn. Các vấn đề tranh luận là không cần thiết, vì quan trọng là chúng ta làm được gì cho cộng đồng.

F đi vào câu hỏi của bạn: một hệ undetectable, có rất nhiều nghĩa, theo F hiểu, có thể là unobservable, có thể unpredictable. Nếu như hệ của bạn, là hệ unpredictable, thì hoàn toàn có thể dùng bộ lọc thích nghi để giải quyết vấn đề. Đó là câu trả lời của F.

Dưới đây miêu tả bằng lời để các bạn khác dễ hình dung.

Đó là, nếu như bây giờ, chúng ta có mô hình của hệ, nhưng không rõ được, mô hình của hệ như thế nào. Nhưng chúng ta biết được rằng, có một vài mô hình khả dĩ nào đó, có thể đại diện cho toàn bộ tập các mô hình có thể cho hệ thống của chúng ta.

Tất cả mọi việc của bộ lọc Kalman, các bạn hiểu đơn giản là việc tìm ra một hệ số Kalman nào đó phù hợp, chúng ta gọi là K.

Khi đó, chúng ta có một số mô hình tham khảo. Mỗi mô hình, chúng ta sẽ tìm được K_1, K_2, K_3... chẳng hạn vậy.

Như vậy, làm sao để ước lượng được K nào là tốt?
Khi đó, chúng ta có thể thấy, một cách ước lượng đơn giản:



khi đó, vòng lặp tìm K cũng sẽ cho chúng ta kết quả, mà chúng ta không cần quan tâm nhiều.

Đối với hệ, undetectable, theo nghĩa unobservable, thì cái này thực sự F chưa tìm hiểu sâu nên không biết, rất mong nếu bạn đã tìm hiểu sâu về Kalman, có thể giúp đỡ mọi người, chúng ta cố gắng thực hiện các bài viết trên tinh thần xây dựng, điều này sẽ tốt cho thành viên rất nhiều.

Hiện nay F đang tập trung vào việc thực hiện dự án điều khiển PID của picvietnam, cho nên tạm thời F chưa tập trung lại về vấn đề Kalman. Nếu như có những gì F còn sai sót, mong bạn giúp đỡ sửa chữa và bổ sung.

Chúc vui

[thanhtung1010]

Vấn đề là mình muốn xác định góc nghiên từ hai cảm biến accelometer và gyro (dùng bộ lọc kalman). Mình chưa hiểu ở chỗ:
- Trong bộ lọc Kalman ma trận R, Q xác định bằng thực nghiệm như thế nào?
- Tín hiệu đọc từ cảm biến accelometer hay gyro dùng để đánh giá giá trị ước lượng "predict" ?
- Mình cũng đọc qua một đoạn code mẫu về bộ lọc Kalman nhưng vẫn không biết sử dụng như thế nào? Có ai biết chỉ mình với!! huhu..

[sunwishbmw]

Các anh thử lấy ví dụ trường hợp nào thực sự cần bộ Kalman này, vì em thấy nó hoạt động phức tạp quá, không biết VĐK bình thường có đáp ứng đủ cái này ko (vì VĐK còn phải làm nhiều cái khác nữa mà).
Hehehe, em đọc Kalman_intro.pdf, có từ này ko dịch đựoc :
"a priori estimate state".

[HaiAu2005]

Có ai có nhu cầu tìm hiểu về lý thuyết lọc thích ứng (Adaptive Filtering Theory) thì download cuốn sách ở địa chỉ sau. Trong cuốn này có Chương 7 viết về các bộ lọc Kalman (Chapter 7 Kalman Filters).

Adaptive Filtering Theory
SBN: 013322760X
Title: Adaptive Filter Theory (3rd Edition)
Author: Simon S. Haykin Simon Haykin
Publisher: Prentice Hall
Publication Date: 1995-12-27
Number Of Pages: 989

Download (91.7MB):
http://e-books.amagrammer.net/%EC%88...3rd%20Ed.).pdf

Download một số sách khác về toán:
http://e-books.amagrammer.net/%EC%88...4%80%EB%A0%A8/

H.A.

[bunyuki]

hê hê Sorry,em nhầm chỗ:E{v.v'}=R.
Trả lời Béo luôn:
Khi tính toán bộ lọc Kalman là phải đưa ra giá trị ước lượng dựa các biến trạng thái trên các thông số tổng hợp của quá trình,đo,mô hình...một cách chân thực nhất để lam đầu vào cho bộ điều khiển.Khi tính toán người ta coi chia thành hai giai đoạn:Predict và Correct.Hai giai đoạn này bổ sung ,tác động lẫn nhau theo 1 vòng tròn khép kín(tao ko vẽ minh hoạ đc) đại loại là đoán trứơc rồi sửa cái đoán ấy cho phù hợp.Cho nên người ta còn gọi KALMAN FILTER là cái ESTIMATOR là vì thế.Trong đó,mỗi một giai đoạn người ta tính toán 1 thông số.Giai đoạn Predict người ta ước lượng trạng thái của hệ thống dựa trên trạng thái trươc đó đã có,cái giá trị ước lượng trong giai đoạn này gọi là 'a priori' tức là trạng thái trước,trạng thái sơ cấp ,trạng thái chưa đc bù kí hiệu là Xk-(a priori thời điểm k):
Xk-=A*x(k-1)^+B*u
Trong giai đoạn này ta tính covariance của sai lệch nhiễu luôn(cũng là trạng thái priori) Pk-=A*Pk-1*A'+Q
Tuy nhiên giá trị priori này chưa mang tính chân thực về hệ thống,và ta cần phải Correct lại cho đúng dựa trên các giá trị đo đc từ các sensor.Đó chính là nhiẹm vụ của giai đoạn Correct(hay update này).Giá trị đc corect lúc này gọi là 'a posteriori' kí hiệu là Xk^:
Xk^=Xk- + K(zk-H*Xk-)
zk:giá trị nhận từ sensor
K là hệ số Kalman phản hồi sai lệch trạng thái.Việc giải K khá phức tạp.Một trong cách đó là giải phương trình Riccacti.Cái này tao có nhưng chắc chẳng cần đọc,hoa mắt chóng mặt lắm.Đại loại là tính K theo covariance của sai lẹch trạng thái như sau:
K=Pk-*H'*inv(H*Pk-*H'+R)
Rồi tính thêm Pk=(I-K*H)*Pk- để cho vòng lặp sau
thế đó,lằng nhằng vậy thôi
khá lằng nhằng nhưng viết ra thấy mình hỉu đôi chút hêhê
Bác FALLEAF đâu nhẩy,lâu lắm ko thấy